Ninety-Nine Swift Problems
Ninety-Nine Swift Problems is a collection of interesting problems (also known as challenges) that will help Swift programmers like you learn and practice your skills in logic programming, data structures and algorithms in the Swift programming language.
This list is an adaptation by me, Eneko Alonso, of the Ninety-Nine Scala Problems written by Phil Gold, which in turn was an adaptation of the original Ninety-Nine Prolog Problems written by Werner Hett at Berne University of Applied Sciences in Berne, Switzerland.
From the original:
The problems have different levels of difficulty. Those marked with a single asterisk (*) are easy. If you have successfully solved the preceding problems you should be able to solve them within a few (say 15) minutes. Problems marked with two asterisks (**) are of intermediate difficulty. If you are a skilled programmer it shouldn’t take you more than 30-90 minutes to solve them. Problems marked with three asterisks (***) are more difficult. You may need more time (i.e. a few hours or more) to find a good solution.
Your goal should be to find the most elegant solution of the given problems. Efficiency is important, but clarity is even more crucial. Some of the (easy) problems can be trivially solved using built-in functions. However, in these cases, you learn more if you try to find your own solution.
I have maintained the difficulties from the Scala and Prolog problems, as they should also apply to Swift. The problem numbers have also been preserved to match the originals, with a few exceptions where I have split the problems in multiple parts.
I recommend you try to solve all these problems by hand, writing your own solutions, while also thinking of performance by avoiding O(n2) solutions. It is fine, however, if you use your solutions from previous problems to solve the following ones.
Problems are divided in seven categories:
Solutions for these problems can be written in Swift by creating a Playground in Xcode. Classes and structures can be placed on the source files folder to keep the Playground clean.
A better way, maybe, would be creating an Xcode project for an iOS, OS X or tvOS application or framework. This would make it very easy to test your solutions with unit tests and code coverage. An OS X command line application would also work, but it will require more configuration to get the unit tests ready.
You can also create Swift files without an Xcode project and use swift or swiftc on the terminal to run the code. Use swift build if you have Swift 2.2 installed.
Section 1: Working with Linked Lists
A list is either empty or it is composed of a first element (head) and a tail, which is a list itself.
We are going to solve the problems on this section by using a generic Linked List, starting with the following signature:
class List<T> {
var value: T
var next: List<T>?
}
The gist List.swift contains the basics of the List class to get you started, including a convenience initializer to create lists in the List(1, 2, 3, ...) form.
Section rules:
- Individual methods or computed properties will be added to the
List<T>class as extensions to solve each problem. - Consider instances of
Listas immutable. All methods should return new instances of linked lists (instead of modifying the current list). - Using sequence types from the Swift Standard Library, like
ArrayorSetis not allowed.
P01 (*) Find the last element of a linked list.
Example:
List(1, 1, 2, 3, 5, 8).last
Result:
8
Implementation:
extension List {
var last: T? {
...
}
}
P02 (*) Find the last but one element of a linked list.
Example:
List(1, 1, 2, 3, 5, 8).pennultimate
Result:
5
Implementation:
extension List {
var pennultimate: T? {
...
}
}
P03 (*) Find the Kth element of a linked list.
By convention, the first element in the list is element 0. Use Swift subscripts to get the value from the linked list.
Example:
let list = List(1, 1, 2, 3, 5, 8)
list[2]
Result:
2
Implementation:
extension List {
subscript(index: Int) -> T? {
...
}
}
P04 (*) Find the number of elements of a linked list.
Example:
List(1, 1, 2, 3, 5, 8).length
Result:
6
Implementation:
extension List {
var length: Int {
...
}
}
P05 (*) Reverse a linked list.
Example:
List(1, 1, 2, 3, 5, 8).reverse()
Result:
List(8, 5, 3, 2, 1, 1)
Implementation:
extension List {
func reverse() {
...
}
}
P06 (*) Find out whether a linked list is a palindrome.
Example:
List(1, 2, 3, 2, 1).isPalindrome()
Result:
true
Implementation:
extension List where T:Equatable {
func isPalindrome() -> Bool {
...
}
}
Note: Requires list elements to conform to Equatable.
P07 (**) Flatten a nested linked list structure.
Example:
List<Any>(List<Any>(1, 1), 2, List<Any>(3, List<Any>(5, 8))).flatten()
Result:
List(1, 1, 2, 3, 5, 8)
Implementation:
extension List {
func flatten() -> List {
...
}
}
P08 (**) Eliminate consecutive duplicates of linked list elements.
If a linked list contains repeated elements they should be replaced with a single copy of the element. The order of the elements should not be changed.
Example:
let list = List("a", "a", "a", "a", "b", "c", "c", "a", "a", "d", "e", "e", "e", "e")
list.compress()
Result:
List("a", "b", "c", "a", "d", "e")
Implementation:
extension List where T: Equatable {
func compress() {
...
}
}
Note: Requires list elements to conform to Equatable.
P09 (**) Pack consecutive duplicates of linked list elements into sub linked lists.
If a list contains repeated elements they should be placed in separate sub linked lists.
Example:
let list = List("a", "a", "a", "a", "b", "c", "c", "a", "a", "d", "e", "e", "e", "e")
list.pack()
Result:
List(List("a", "a", "a", "a"), List("b"), List("c", "c"), List("a", "a"), List("d"), List("e", "e", "e", "e"))
Implementation:
extension List where T: Equatable {
func pack() -> List<List<T>> {
...
}
}
Note: Requires list elements to conform to Equatable.
P10 (*) Run-length encoding of a linked list.
Use the result of problem P09 to implement the so-called run-length encoding data compression method. Consecutive duplicates of elements are encoded as tuples (N, E) where N is the number of duplicates of the element E.
Example:
let list = List("a", "a", "a", "a", "b", "c", "c", "a", "a", "d", "e", "e", "e", "e")
list.encode()
Result:
List((4, "a"), (1, "b"), (2, "c"), (2, "a"), (1, "d"), (4, "e"))
Implementation:
extension List where T: Equatable {
func encode() -> List<(Int, T)> {
...
}
}
Note: Requires list elements to conform to Equatable.
P11 (*) Modified run-length encoding.
Modify the result of problem P10 in such a way that if an element has no duplicates it is simply copied into the result linked list. Only elements with duplicates are transferred as (N, E) terms.
Example:
let list = List("a", "a", "a", "a", "b", "c", "c", "a", "a", "d", "e", "e", "e", "e")
list.encodeModified()
Result:
List((4, "a"), "b", (2, "c"), (2, "a"), "d", (4, "e"))
Implementation:
extension List where T: Equatable {
func encodeModified() -> List<Any> {
...
}
}
Note: Requires list elements to conform to Equatable.
P12 (**) Decode a run-length encoded linked list.
Given a run-length code linked list generated as specified in problem P10, construct its uncompressed version.
Example:
let list = List((4, "a"), (1, "b"), (2, "c"), (2, "a"), (1, "d"), (4, "e"))
list.decode()
Result:
List("a", "a", "a", "a", "b", "c", "c", "a", "a", "d", "e", "e", "e", "e")
Implementation:
extension List {
func decode() -> List<String> {
...
}
}
Note: Implement for String only.
P13 (**) Run-length encoding of a linked list (direct solution).
Implement the so-called run-length encoding data compression method directly. I.e. don’t use other methods you’ve written (like P09’s pack); do all the work directly.
Example:
let list = List("a", "a", "a", "a", "b", "c", "c", "a", "a", "d", "e", "e", "e", "e")
list.encodeDirect()
Result:
List((4, "a"), (1, "b"), (2, "c"), (2, "a"), (1, "d"), (4, "e"))
Implementation:
extension List where T: Equatable {
func encodeDirect() -> List<(Int, T)> {
...
}
}
Note: Requires list elements to conform to Equatable.
P14 (*) Duplicate the elements of a linked list.
Example:
let list = List("a", "b", "c", "c", "d")
list.duplicate()
Result:
List("a", "a", "b", "b", "c", "c", "c", "c", "d", "d")
Implementation:
extension List {
func duplicate() -> List {
...
}
}
P15 (**) Duplicate the elements of a linked list a given number of times.
Example:
let list = List("a", "b", "c", "c", "d")
list.duplicate(3)
Result:
List("a", "a", "a", "b", "b", "b", "c", "c", "c", "c", "c", "c", "d", "d", "d")
Implementation:
extension List {
func duplicate(times: Int) -> List {
...
}
}
P16 (**) Drop every Nth element from a linked list.
Example:
let list = List("a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k")
list.drop(3)
Result:
List("a", "b", "d", "e", "g", "h", "j", "k")
Implementation:
extension List {
func drop(every: Int) -> List? {
...
}
}
P17 (*) Split a linked list into two parts.
The length of the first part is given. Use a Tuple for your result.
Example:
let list = List("a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k")
list.split(3)
Result:
(List("a", "b", "c"), List("d", "e", "f", "g", "h", "i", "j", "k"))
Implementation:
extension List {
func split(atIndex: Int) -> (left: List, right: List) {
...
}
}
P18 (**) Extract a slice from a linked list.
Given two indices, I and K, the slice is the linked list containing the elements from and including the Ith element up to but not including the Kth element of the original linked list. Start counting the elements with 0.
Example:
let list = List("a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k")
list.slice(3, 7)
Result:
List("d", "e", "f", "g")
Implementation:
extension List {
func slice(from: Int, _ to: Int) -> List {
...
}
}
P19 (**) Rotate a list N places to the left.
Example #1:
let list = List("a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k")
list.rotate(3)
Result:
List("d", "e", "f", "g", "h", "i", "j", "k", "a", "b", "c")
Example #2:
let list = List("a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k")
list.rotate(-2)
Result:
List("j", "k", "a", "b", "c", "d", "e", "f", "g", "h", "i")
Implementation:
extension List {
func rotate(amount: Int) -> List {
...
}
}
P20 (*) Remove the Kth element from a linked list.
Return a linked list without the removed element and the removed element in a Tuple. Elements are numbered from 0.
Example:
let list = List("a", "b", "c", "d")
list.removeAt(1)
Result:
(List("a", "c", "d"), "b")
Implementation:
extension List {
func removeAt(position: Int) -> (rest: List?, removed: T?) {
...
}
}
P21 (*) Insert an element at a given position into a linked list.
Example:
let list = List("a", "b", "c", "d")
list.insertAt(1, "new")
Result:
List("a", "new", "b", "c", "d")
Implementation:
extension List {
func insertAt(index: Int, _ value: T) {
...
}
}
P22 (*) Create a linked list containing all integers within a given range.
Example:
List.range(4, 9)
Result:
List(4, 5, 6, 7, 8, 9)
Implementation:
extension List {
class func range(from: Int, _ to: Int) -> List<Int> {
...
}
}
Note: Implement as class function.
P23 (**) Extract a given number of randomly selected elements from a linked list.
Example:
let list = List("a", "b", "c", "d", "e", "f", "g", "h")
list.randomSelect(3)
Result:
List("e", "d", "a")
Implementation:
extension List {
func randomSelect(amount: Int) -> List {
...
}
}
Hint #1: Use the solution to problem P20.
Hint #2: Use the provided randomInt(under:) function for Linux support.
P24 (*) Lotto: Draw N different random numbers from the set 1..M.
Return a linked list with the lotto numbers.
Example:
List.lotto(6, 49)
Result:
List(23, 1, 17, 33, 21, 37)
Implementation:
extension List {
class func lotto(numbers: Int, _ maximum: Int) -> List<Int> {
...
}
}
Note: Implement as class function.
P25 (*) Generate a random permutation of the elements of a linked list.
Example:
List("a", "b", "c", "d", "e", "f").randomPermute()
Result:
List("b", "a", "d", "c", "e", "f")
Implementation:
extension List {
func randomPermute() -> List {
...
}
}
Hint: Use the solution of problem P23.
P26 (**) Generate the combinations of K distinct objects chosen from the N elements of a linked list.
In how many ways can a committee of 3 be chosen from a group of 12 people? We all know that there are C(12,3) = 220 possibilities (C(N,K) denotes the well-known binomial coefficient). For pure mathematicians, this result may be great. But we want to really generate all the possibilities.
Example:
List("a", "b", "c").combinations(2)
Result:
List(List("a", "b"), List("a", "c"), List("b", "c"))
Implementation:
extension List {
func combinations(group: Int) -> List<List<T>> {
...
}
}
P26B (**) Generate the permutations of K distinct objects chosen from the N elements of a linked list.
In how many ways can 12 people sit on 3 chairs? Generate all the possible permutations. Eg. P(12,3) = 660.
Example:
List("a", "b", "c").permutations(2)
Result:
List(List("a", "b"), List("a", "c"), List("b", "a"), List("b", "c"), List("c", "a"), List("c", "b"))
Implementation:
extension List {
func permutations(group: Int) -> List<List<T>> {
...
}
}
P27 (**) Group the elements of a set into disjoint subsets.
In how many ways can a group of 9 people work in 3 disjoint subgroups of 2, 3 and 4 persons? Write a function that generates all the possibilities.
Example:
let list = List("Aldo", "Beat", "Carla", "David", "Evi", "Flip", "Gary", "Hugo", "Ida")
list.group3()
Result:
List(List(List("Aldo", "Beat"), List("Carla", "David", "Evi"), List("Flip", "Gary", "Hugo", "Ida")), ...)
Implementation:
extension List {
func group3() -> List<List<List<T>>> {
...
}
}
Note that we do not want permutations of the group members; i.e. ((Aldo, Beat), …) is the same solution as ((Beat, Aldo), …). However, we make a difference between ((Aldo, Beat), (Carla, David), …) and ((Carla, David), (Aldo, Beat), …).
You may find more about this combinatorial problem in a good book on discrete mathematics under the term “multinomial coefficients”.
P27B (**) Group the elements of a set into disjoint subsets - Part 2.
Generalize the above predicate in a way that we can specify a list of group sizes and the predicate will return a list of groups.
Example:
let list = List("Aldo", "Beat", "Carla", "David", "Evi", "Flip", "Gary", "Hugo", "Ida")
list.group(List(2, 2, 5))
Result:
List(List(List("Aldo", "Beat"), List("Carla", "David"), List("Evi", "Flip", "Gary", "Hugo", "Ida")), ...)
Implementation:
extension List {
func group(groups: List<Int>) -> List<List<List<T>>> {
...
}
}
P28 (**) Sorting a linked list of linked lists according to length of sublists.
We suppose that a linked list contains elements that are linked lists themselves. The objective is to sort the elements of the list according to their length. E.g. short lists first, longer lists later, or vice versa.
Example:
let list = List(List("a", "b", "c"), List("d", "e"), List("f", "g", "h"), List("d", "e"), List("i", "j", "k", "l"), List("m", "n"), List("o"))
list.lsort()
Result:
List(List("o"), List("d", "e"), List("d", "e"), List("m", "n"), List("a", "b", "c"), List("f", "g", "h"), List("i", "j", "k", "l"))
Implementation:
extension List {
func lsort() -> List {
...
}
}
P28B (**) Sorting a linked list of linked lists according to their length frequency.
Again, we suppose that a list contains elements that are lists themselves. But this time the objective is to sort the elements according to their length frequency; i.e. in the default, sorting is done ascendingly, lists with rare lengths are placed, others with a more frequent length come later.
Example:
let list = List(List("a", "b", "c"), List("d", "e"), List("f", "g", "h"), List("d", "e"), List("i", "j", "k", "l"), List("m", "n"), List("o"))
list.lsortFreq()
Result:
List(List("i", "j", "k", "l"), List("o"), List("a", "b", "c"), List("f", "g", "h"), List("d", "e"), List("d", "e"), List("m", "n"))
Implementation:
extension List {
func lsortFreq() -> List {
...
}
}
Note that in the above example, the first two lists in the result have length 4 and 1 and both lengths appear just once. The third and fourth lists have length 3 and there are two list of this length. Finally, the last three lists have length 2. This is the most frequent length.
Apendix 1A (**) Sequences.
Now that you have solved all the linked list problems above, implement the SequenceType protocol on our List class.
Implementation:
extension List: SequenceType {
func generate() -> AnyGenerator<T> {
...
}
}
This will give our class instant access to the following Swift 2.1 methods: contains, enumerate, dropFirst, dropLast, elementsEqual, enumerate, filter, flatMap, flatten, forEach, generate, joinWithSeparator, lexicographicalCompare, map, maxElement, minElement, prefix, reduce, reverse, sort, split, startsWith, suffix and understimateCount.
These methods might be useful in the following sections.
Section 2: Arithmetic
For the next section, we’re going to take a different tack with the solutions. Instead of using a class, we will define the solutions as extensions to Int (both instance and class methods).
P31 (**) Determine whether a given integer number is prime.
Example:
7.isPrime()
Result:
true
Implementation:
extension Int {
func isPrime() -> Bool {
...
}
}
P32 (**) Determine the greatest common divisor of two positive integer numbers.
Use Euclid’s algorithm.
Example:
Int.gcd(36, 63)
Result:
9
Implementation:
extension Int {
class func gcd(first: Int, _ second: Int) -> Int {
...
}
}
P33 (*) Determine whether two positive integer numbers are coprime.
Two numbers are coprime if their greatest common divisor equals 1.
Example:
35.isCoprimeTo(64)
Result:
true
Implementation:
extension Int {
func isCoprimeTo(other: Int) -> Bool {
...
}
}
P34 (**) Calculate Euler’s totient function phi(m).
Euler’s so-called totient function phi(m) is defined as the number of positive integers r (1 <= r <= m) that are coprime to m.
E.g. m = 10: r = 1,3,7,9; thus phi(m) = 4. Note the special case: phi(1) = 1.
Example:
10.totient
Result:
4
Implementation:
extension Int {
var totient: Int {
...
}
}
P35 (**) Determine the prime factors of a given positive integer.
Construct a flat linked list containing the prime factors in ascending order.
Example:
315.primeFactors
Result:
List(3, 3, 5, 7)
Implementation:
extension Int {
var primeFactors: List<Int> {
...
}
}
P36 (**) Determine the prime factors of a given positive integer - Part 2.
Construct a linked list containing tuples with the prime factors and their multiplicity.
Example:
315.primeFactorMultiplicity
Result:
List((3, 2), (5, 1), (7, 1))
Implementation:
extension Int {
var primeFactorMultiplicity: List<(Int, Int)> {
...
}
}
Alternatively, use a Dictionary for the result.
Example:
315.primeFactorMultiplicityDict
Result:
Dictionary([3: 2, 5: 1, 7: 1])
Implementation:
extension Int {
var primeFactorMultiplicityDict: Dictionary<Int, Int> {
...
}
}
P37 (**) Calculate Euler’s totient function phi(m) (improved).
See problem P34 for the definition of Euler’s totient function. If the list of the prime factors of a number m is known in the form of problem P36 then the function phi(m) can be efficiently calculated as follows: Let [[p1, m1], [p2, m2], [p3, m3], ...] be the list of prime factors (and their multiplicities) of a given number m. Then phi(m) can be calculated with the following formula:
phi(m) = (p1-1)*p1(m1-1) * (p2-1)*p2(m2-1) * (p3-1)*p3(m3-1) * …
Implementation:
extension Int {
var totientImproved: Int {
...
}
}
P38 (*) Compare the two methods of calculating Euler’s totient function.
Use the solutions of problems P34 and P37 to compare the algorithms. Try to calculate phi(10090) as an example.
P39 (*) A linked list of prime numbers.
Given a range of integers by its lower and upper limit, construct a linked list of all prime numbers in that range.
Example:
Int.listPrimesinRange(7...31)
Result:
List(7, 11, 13, 17, 19, 23, 29, 31)
Implementation:
extension Int {
class func listPrimesInRange(range: Range<Int>) -> List<Int> {
...
}
}
P40 (**) Goldbach’s conjecture.
Goldbach’s conjecture says that every positive even number greater than 2 is the sum of two prime numbers. E.g. 28 = 5 + 23. It is one of the most famous facts in number theory that has not been proved to be correct in the general case. It has been numerically confirmed up to very large numbers (much larger than Swift’s Int can represent). Write a function to find two prime numbers that sum up to a given even integer.
Example:
28.goldbach()
Result:
(5, 23)
Implementation:
extension Int {
func goldbach() -> (Int, Int) {
...
}
}
P41 (**) A list of Goldbach compositions.
Given a range of integers by its lower and upper limit, print a list of all even numbers and their Goldbach composition.
Example:
Int.printGoldbachList(9...20)
Output:
10 = 3 + 7
12 = 5 + 7
14 = 3 + 11
16 = 3 + 13
18 = 5 + 13
20 = 3 + 17
Implementation:
extension Int {
class func printGoldbachList() {
...
}
}
P41B (**) A list of Goldbach compositions (limited).
In most cases, if an even number is written as the sum of two prime numbers, one of them is very small. Very rarely, the primes are both bigger than, say, 50. Try to find out how many such cases there are in the range 2...3000.
Example (minimum value of 50 for the primes):
Int.printGoldbachListLimited(1...2000, 50)
Output:
992 = 73 + 919
1382 = 61 + 1321
1856 = 67 + 1789
1928 = 61 + 1867
Implementation:
extension Int {
class func printGoldbachListLimited() {
...
}
}
Section 3: Logic and Codes
Because this is a short section, we will create global functions.
P46 (**) Truth tables for logical expressions.
Define functions and, or, nand, nor, xor, impl, and equ (for logical equivalence) which return true or false according to the result of their respective operations; e.g. and(A, B) is true if and only if both A and B are true.
and- Logical Conjunction ANDor- Logical Disjunction ORnand- Logical NANDnor- Logical NORxor- Exclusive Disjunction XORimpl- Logical Implicationequ- Logical Equality XNOR
Example #1:
and(true, true)
Result:
true
Example #2:
xor(true, true)
Result:
false
Implementation:
func and(a: Bool, _ b: Bool) -> Bool) {
...
}
A logical expression in two variables can be written as a closure in Swift with two parameters:
{ (a: Bool, b: Bool) -> Bool in and(or(a, b), nand(a, b)) }
{ (a, b) in and(or(a, b), nand(a, b)) } // Type Inference
{ and(or($0, $1), nand($0, $1)) } // Shorthand Argument Names
Now, write a function called table which generates the truth table of a given logical expression in two variables and returns it as a series of linked lists.
Example:
table({ and($0, or($0, $1)) })
Result:
// (A, B, Result)
List(
List(true, true, true ),
List(true, false, true ),
List(false, true, false),
List(false, false, false)
)
Implementation:
func table(expression: (a: Bool, b: Bool) -> Bool) -> List<List<Bool>> {
...
}
P47 (*) Truth tables for logical expressions - Part 2.
Continue problem P46 by redefining and, or, etc. as infix operators with left associativity and the corresponding precedence.
Use the following list of mathematical symbols:
∧- Logical Conjunction AND∨- Logical Disjunction OR⊼- Logical NAND⊽- Logical NOR⊕- Exclusive Disjunction XOR→- Logical Implication≡- Logical Equality XNOR
Example:
table({ $0 ∧ ($0 ∨ $1) })
Result:
// (A, B, Result)
List(
List(true, true, true ),
List(true, false, true ),
List(false, true, false),
List(false, false, false)
)
Use the following operator precedences:
and,nand=> 120or,nor,xor,xnor,impl,equ=> 110
P48 (**) Truth tables for logical expressions - Part 3.
Generalize problem P47 in such a way that the logical expression may contain any number of logical variables. Define table in a way that table(variableNum, expression) generates the truth table for the expression for all the logical variables, and returns it as a series of linked lists.
Example:
table(3, expression: { vars in vars[0] ∧ vars[1] ∨ vars[2] })
Result:
// (A, B, C, Result)
List(
List(true, true, true, true ),
List(true, true, false, true ),
List(true, false, true, true ),
List(true, false, false, false),
List(false, true, true, true ),
List(false, true, false, false),
List(false, false, true, true ),
List(false, false, false, false)
)
Implementation:
func table(variables: Int, expression: (vars: [Bool]) -> Bool) -> List<List<Bool>> {
...
}
P49 (**) Gray code.
An n-bit Gray code is a sequence of n-bit strings constructed according to certain rules. For example,
n = 1: C(1) = ("0", "1").
n = 2: C(2) = ("00", "01", "11", "10").
n = 3: C(3) = ("000", "001", "011", "010", "110", "111", "101", "100").
Find out the construction rules and write a function to generate Gray codes.
Example:
gray(3)
Result:
List("000", "001", "011", "010", "110", "111", "101", "100")
Implementation:
func gray(number: Int) -> List<String> {
...
}
See if you can use memoization to make the function more efficient.
P50 (***) Huffman code.
First of all, consult a good book on discrete mathematics or algorithms for a detailed description of Huffman codes!
We suppose a set of symbols with their frequencies, given as a list of (S, F) Tuples. E.g. (("a", 45), ("b", 13), ("c", 12), ("d", 16), ("e", 9), ("f", 5)). Our objective is to construct a linked list of (S, C) Tuples, where C is the Huffman code word for the symbol S.
Example:
huffman(List(("a", 45), ("b", 13), ("c", 12), ("d", 16), ("e", 9), ("f", 5)))
Result:
List(("a", "0"), ("b", "101"), ("c", "100"), ("d", "111"), ("e", "1101"), ("f", "1100"))
Implementation:
func huffman(symbols: List<(String, Int)>) -> List<(String, String)> {
...
}
Section 4: Binary Trees
A binary tree is either empty or it is composed of a root element and two successors, which are binary trees themselves.
We will define our generic tree as follows:
class Tree<T> {
let value: T
var left: Tree<T>?
var right: Tree<T>?
init(_ value: T, _ left: Tree<T>? = nil, _ right: Tree<T>? = nil) {
self.value = value
self.left = left
self.right = right
}
}
A tree with only a root node would be Tree("a") and an empty tree would be nil.
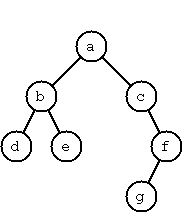
The example tree above is given by:
Tree("a", Tree("b", Tree("d"), Tree("e")), Tree("c", nil, Tree("f", Tree("g"), nil)))
Throughout this section, we will be adding methods to the Tree class above as extensions to solve each problem.
Leaf nodes (nodes with no subtrees) will be displayed in the results below as Tree("a") instead of Tree("a", nil, nil). However, nodes with one subtree will always display the tree constructor parameters.
P54 (*) Completely balanced trees.
In a completely balanced binary tree, the following property holds for every node: The number of nodes in its left subtree and the number of nodes in its right subtree are almost equal, which means their difference is not greater than one (do not confuse with height-balanced trees where the difference in height is less or equal than one).
Example:
Tree(1, Tree(2), Tree(3)).isCompletelyBalanced()
Result:
true
Implementation:
extension Tree {
func isCompletelyBalanced() -> Bool {
...
}
}
Note: Original problem ‘P54 Check whether a given term represents a binary tree’ does not apply to Swift, since our tree representation will only allow well-formed trees.
P55 (**) Construct completely balanced binary trees.
Write a class method Tree<T>.makeBalancedTrees() to construct completely balanced binary trees for a given number of nodes. The function should generate all solutions, returning them on a linked list. The function should take as parameters the number of nodes and a single value to put in all of them.
Example:
Tree.makeBalancedTrees(nodes: 4, value: "x")
Result:
List(
Tree("x", Tree("x"), Tree("x", nil, Tree("x"))),
Tree("x", Tree("x"), Tree("x", Tree("x"), nil)),
Tree("x", Tree("x", nil, Tree("x")), Tree("x")),
Tree("x", Tree("x", Tree("x"), nil), Tree("x"))
)
Implementation:
extension Tree {
class func makeBalancedTrees(nodes nodes: Int, value: T) -> List<Tree<T>>? {
...
}
}
P56 (**) Symmetric binary trees.
Let us call a binary tree symmetric if you can draw a vertical line through the root node and then the right subtree is the mirror image of the left subtree. Add an isSymmetric() method to the Tree class to check whether a given binary tree is symmetric.
Hint: Write an isMirrorOf() method first to check whether one tree is the mirror image of another. We are only interested in the structure, not in the contents of the nodes.
Example:
Tree("a", Tree("b"), Tree("c")).isSymmetric()
Result:
true
Implementation:
extension Tree {
func isSymetric() -> Bool {
...
}
}
P57 (**) Binary search trees.
Write a function to add an element to a binary search tree.
Example:
let tree = Tree(2)
tree.addValue(3)
Result:
Tree(2, nil, Tree(3))
Continue:
tree.addValue(0)
Result:
Tree(2, Tree(0), Tree(3))
Implementation:
extension Tree {
func addValue(value: T) -> Tree {
...
}
}
P57B (**) Binary search trees from Linked List.
Use the function from P57 to construct a binary tree from a list of integers. Define a convenience initializer as follows:
Example:
Tree(list: List(3, 2, 5, 7, 1))
Result:
Tree(3, Tree(2, Tree(1), nil), Tree(5, nil, Tree(7)))
Implementation:
extension Tree {
convenience init(list: List<T>) {
...
}
}
Then, use this initializer to test your solution to P56.
Example:
Tree(list: List(5, 3, 18, 1, 4, 12, 21)).isSymmetric()
Result:
true
Example:
Tree(list: List(3, 2, 5, 7, 4)).isSymmetric()
Result:
false
P58 (**) Generate-and-test paradigm.
Apply the generate-and-test paradigm to construct all symmetric, completely balanced binary trees with a given number of nodes.
Example:
Tree.makeSymmetricBalancedTrees(nodes: 5, value: "x")
Result:
List(
Tree("x", Tree("x", nil, Tree("x")), Tree("x", Tree("x"), nil)),
Tree("x", Tree("x", Tree("x"), nil), Tree("x", nil, Tree("x")))
)
Implementation:
extension Tree {
class func makeSymmetricBalancedTrees(nodes nodes: Int, value: T) -> List<Tree<T>>? {
...
}
}
P59 (**) Construct height-balanced binary trees.
In a height-balanced binary tree, the following property holds for every node: The height of its left subtree and the height of its right subtree are almost equal, which means their difference is not greater than one.
Write a method Tree<T>.makeHeightBalancedTrees() to construct height-balanced binary trees for a given height with a supplied value for the nodes. The function should generate all solutions.
Example:
Tree.makeHeightBalancedTrees(height: 3, value: "x")
Result:
List(
Tree("x", Tree("x", Tree("x"), Tree("x")), Tree("x", Tree("x"), Tree("x"))),
Tree("x", Tree("x", Tree("x"), Tree("x")), Tree("x", Tree("x"), nil),
...
)
Implementation:
extension Tree {
class func makeHeightBalancedTrees(height height: Int, value: T) -> List<Tree<T>>? {
...
}
}
P60 (**) Construct height-balanced binary trees with a given number of nodes.
Consider a height-balanced binary tree of height h. What is the maximum number of nodes it can contain? Clearly, MaxN = 2h - 1. However, what is the minimum number MinN? This question is more difficult. Try to find a recursive statement and turn it into a function minNodesForBalancedTreeOfHeight() that takes a height and returns MinN.
Example:
minNodesForBalancedTreeOfHeight(3)
Result:
4
On the other hand, we might ask: what is the maximum height h a height-balanced binary tree with n nodes can have? Write a maxHeightForBalancedTreeWithNodeCount() function.
Example:
maxHeightForBalancedTreeWithNodeCount(4)
Result:
3
Now, we can attack the main problem: construct all the height-balanced binary trees with a given number of nodes.
Example:
Tree.makeHeightBalancedTrees(nodes: 4, value: "x")
Result:
List(
Tree("x", Tree("x", Tree("x"), nil), Tree("x"),
Tree("x", Tree("x", nil, Tree("x")), Tree("x"),
...
)
Implementation:
extension Tree {
class func makeHeightBalancedTrees(nodes nodes: Int, value: T) -> List<Tree<T>>? {
...
}
}
Find out how many height-balanced trees exist for N = 15.
P61 (*) Count the leaves of a binary tree.
A leaf is a node with no successors. Write a computed property leafCount to count them.
Example:
Tree("x", Tree("x"), nil).leafCount
Result:
1
Implementation:
extension Tree {
var leafCount: Int {
...
}
}
P61B (*) Collect the leaves of a binary tree in a linked list.
A leaf is a node with no successors. Write a method leaves() to collect them in a linked list.
Example:
Tree("a", Tree("b"), Tree("c", Tree("d"), Tree("e"))).leaves()
Result:
List("b", "d", "e")
Implementation:
extension Tree {
func leaves() -> List<T> {
...
}
}
P62 (*) Collect the internal nodes of a binary tree in a linked list.
An internal node of a binary tree has either one or two non-empty successors. Write a method internalNodes() to collect them in a linked list.
Example:
Tree("a", Tree("b"), Tree("c", Tree("d"), Tree("e"))).internalNodes()
Result:
List("a", "c")
Implementation:
extension Tree {
func internalNodes() -> List<T> {
...
}
}
P62B (*) Collect the nodes at a given level in a linked list.
A node of a binary tree is at level n if the path from the root to the node has length n-1. The root node is at level 1. Write a method nodesAtLevel() to collect all nodes at a given level in a linked list.
Example:
Tree("a", Tree("b"), Tree("c", Tree("d"), Tree("e"))).nodesAtLevel(2)
Result:
List("b", "c")
Implementation:
extension Tree {
func nodesAtLevel() -> List<T> {
...
}
}
Using nodesAtLevel() it is easy to construct a method levelOrder() which creates the level-order sequence (traversal) of the nodes. However, there are more efficient ways to do that.
P63 (**) Construct a complete binary tree.
A complete binary tree with height h is defined as follows: The levels 1,2,3,…,h-1 contain the maximum number of nodes (i.e 2(i-1) at the level i, note that we start counting the levels from 1 at the root). In level h, which may contain less than the maximum possible number of nodes, all the nodes are “left-adjusted”. This means that in a level-order tree traversal all internal nodes come first, the leaves come second, and empty successors (the nils which are not really nodes!) come last.
Particularly, complete binary trees are used as data structures (or addressing schemes) for heaps.
We can assign an address number to each node in a complete binary tree by enumerating the nodes in level-order, starting at the root with number 1. In doing so, we realize that for every node x with address a the following property holds: The address of x left and right successors are 2*a and 2*a+1, respectively, supposed the successors do exist. This fact can be used to elegantly construct a complete binary tree structure. Write a method makeCompleteBinaryTree() that takes as parameters the number of nodes and the value to put in each node.
Example:
Tree.makeCompleteTree(nodes: 6, value: "x")
Result:
Tree("x", Tree("x", Tree("x"), Tree("x")), Tree("x", T("x"), nil))
Implementation:
extension Tree {
class func makeCompleteTree(nodes nodes: Int, value: T) -> Tree<T>? {
...
}
}
P64 (**) Layout a binary tree.
As a preparation for drawing a tree, a layout algorithm is required to determine the position of each node in a rectangular grid. Several layout methods are conceivable, one of them is shown in the illustration below.
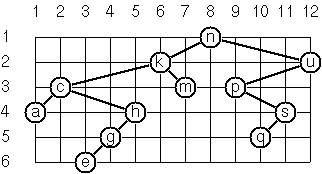
In this layout strategy, the position of a node v is obtained by the following two rules:
- x(v) is equal to the position of the node v in the in-order sequence
- y(v) is equal to the depth of the node v in the tree
In order to store the position of the nodes, we add a new class with the additional information.
public class PositionedTree<T> : Tree<T> {
var x: Int
var y: Int
public init(x: Int, y: Int, value: T, _ left: Tree<T>? = nil, _ right: Tree<T>? = nil) {
self.x = x
self.y = y
super.init(value, left, right)
}
}
Write a method layoutBinaryTree() that turns a tree of normal Tree nodes into a tree of PositionedTree nodes.
Example:
Tree("a", Tree("b", nil, Tree("c")), Tree("d")).layoutBinaryTree()
Result:
PositionedTree(x: 3, y: 1, value: "a",
PositionedTree(x: 1, y: 2, value: "b",
nil,
PositionedTree(x: 2, y: 3, value: "c")
),
PositionedTree(x: 4, y: 2, value: "d")
)
Implementation:
extension Tree {
func layoutBinaryTree() -> PositionedTree<T> {
...
}
}
The tree at the beginning of the problem may be constructed with:
Tree(list: List("n", "k", "m", "c", "a", "h", "g", "e", "u", "p", "s", "q"))
Use it to check your code.
P65 (**) Layout a binary tree - Part 2.
An alternative layout method is depicted in the following illustration. Find out the rules and write the corresponding method.
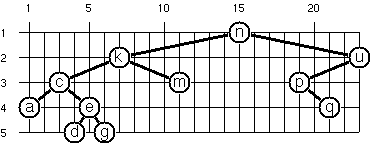
Hint: On a given level, the horizontal distance between neighboring nodes is constant. Use the same conventions as in problem P64.
Example:
Tree("a", Tree("b", nil, Tree("c")), Tree("d")).layoutBinaryTree2()
Result:
PositionedTree(x: 3, y: 1, value: "a",
PositionedTree(x: 1, y: 2, value: "b",
nil,
PositionedTree(x: 2, y: 3, value: "c")
),
PositionedTree(x: 5, y: 2, value: "d")
)
Implementation:
extension Tree {
func layoutBinaryTree2() -> PositionedTree<T> {
...
}
}
The tree at the beginning of the problem may be constructed with:
Tree(list: List("n", "k", "m", "c", "a", "e", "d", "g", "u", "p", "q"))
Use it to check your code.
P66 (***) Layout a binary tree - Part 3.
Yet another layout strategy is shown in the following illustration. The method yields a very compact layout while maintaining a certain symmetry in every node. Find out the rules and write the corresponding method.
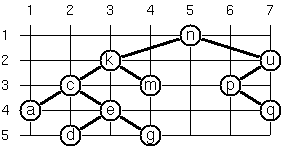
Hint: Consider the horizontal distance between a node and its successor nodes. How tight can you pack together two subtrees to construct the combined binary tree? Use the same conventions as in problem P64 and P65. Note: This is a difficult problem. Don’t give up too early!
Example:
Tree("a", Tree("b", nil, Tree("c")), Tree("d")).layoutBinaryTree3()
Result:
PositionedTree(x: 2, y: 1, value: "a",
PositionedTree(x: 1, y: 2, value: "b",
nil,
PositionedTree(x: 2, y: 3, value: "c")
),
PositionedTree(x: 3, y: 2, value: "d")
)
Implementation:
extension Tree {
func layoutBinaryTree3() -> PositionedTree<T> {
...
}
}
Which layout do you like most?
P67 (**) A string representation of binary trees.

Somebody represents binary trees as strings of the following type:
a(b(d,e),c(,f(g,)))
Implement the CustomStringConvertible protocol to generate this string representation, if the tree is given as usual (using our Tree class).
Example:
Tree("a", Tree("b", Tree("d"), Tree("e")), Tree("c", nil, Tree("f", Tree("g"), nil))).description
Result:
"a(b(d,e),c(,f(g,)))"
Implementation:
extension Tree: CustomStringConvertible {
var description: String {
...
}
}
P67B (**) Construct a binary tree from a string representation.
Write a new convenience initializer which does the inverse of P67; i.e. given the string representation, construct the tree in the usual form.
Example:
Tree(string: "a(b(d,e),c(,f(g,)))")
Result:
Tree("a", Tree("b", Tree("d"), Tree("e")), Tree("c", nil, Tree("f", Tree("g"), nil)))
Implementation:
extension Tree {
convenience init(string: String) {
...
}
}
For simplicity, suppose the information in the nodes is a single letter and there are no spaces in the string.
P68 (**) Pre-order and in-order sequences of binary trees.
We consider binary trees with nodes that are identified by single lower-case letters, as in the example of problem P67.
Write methods preOrder() and inOrder() that construct the pre-order and in-order sequence of a given binary tree, respectively. The results should be linked lists, e.g. List("a", "b", "d", "e", "c", "f", "g") for the pre-order sequence of the example in problem P67.
Pre-order example:
Tree(string: "a(b(d,e),c(,f(g,)))").preOrder()
Result:
List("a", "b", "d", "e", "c", "f", "g")
Implementation:
extension Tree {
func preOrder() -> List<T> {
...
}
}
In-order example:
Tree(string: "a(b(d,e),c(,f(g,)))").inOrder()
Result:
List("d", "b", "e", "a", "c", "g", "f")
Implementation:
extension Tree {
func inOrder() -> List<T> {
...
}
}
P68B (**) Construct a binary tree from pre-order and in-order sequences.
If both the pre-order sequence and the in-order sequence of the nodes of a binary tree are given, then the tree is determined unambiguously. Write a new convenience initializer that does the job.
Example:
Tree(
preOrder: List("a", "b", "d", "e", "c", "f", "g"),
inOrder: List("d", "b", "e", "a", "c", "g", "f")
)
Result:
Tree("a", Tree("b", Tree("d"), Tree("e")), Tree("c", nil, Tree("f", Tree("g"), nil)))
Implementation:
extension Tree {
convenience init(preOrder: List<T>, inOrder: List<T>) {
...
}
}
What happens if the same character appears in more than one node? Try, for instance, Tree(preOrder: List("a", "b", "a"), inOrder: List("b", "a", "a")).
P69 (**) Dotstring representation of binary trees.
We consider again binary trees with nodes that are identified by single lower-case letters, as in the example of problem P67. Such a tree can be represented by the pre-order sequence of its nodes in which dots . are inserted where an empty subtree (nil) is encountered during the tree traversal.
For example, the tree shown in problem P67 is represented as "abd..e..c.fg...". First, try to establish a syntax (BNF or syntax diagrams) and then write a method toDotstring() to convert the tree to Dotstring format.
Example:
Tree(string: "a(b(d,e),c(,f(g,)))").toDotstring()
Result:
"abd..e..c.fg..."
Implementation:
extension Tree {
func toDotstring() -> String {
...
}
}
P69B (**) Construct a binary tree from a Dotstring representation.
Now, write another convenience initializer to construct a tree from a given string in Dotstring format.
Example:
Tree(dotstring: "abd..e..c.fg...")
Result:
Tree("a", Tree("b", Tree("d"), Tree("e")), Tree("c", nil, Tree("f", Tree("g"), nil)))
Implementation:
extension Tree {
convenience init(dotstring: String) {
...
}
}
Apendix 4A (**) Sequences.
Implement the SequenceType protocol on our Tree class to return all the nodes following the in-order traversal sequence.
Implementation:
extension Tree: SequenceType {
func generate() -> AnyGenerator<T> {
...
}
}
Section 5: Multiway Trees
A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest.
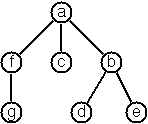
We will implement our multiway trees as follows:
class MTree<T> {
let value: T
var children: List<MTree<T>>?
init(_ value: T, _ children: List<MTree<T>>? = nil) {
...
}
}
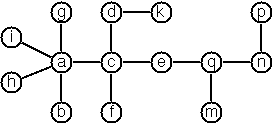
The example tree from the image above is:
MTree("a", List(MTree("f", List(MTree("g"))), MTree("c"), MTree("b", List(MTree("d"), MTree("e")))))
P70B (*) Check whether a given term represents a multiway tree.
Omitted; we can only create well-formed trees.
P70C (*) Count the nodes of a multiway tree.
Write a computed variable nodeCount which counts the nodes of a given multiway tree.
Example:
MTree("a", List(MTree("f"))).nodeCount
Result:
2
Implementation:
extension MTree {
var nodeCount: Int {
...
}
}
P70 (**) Tree construction from a node string.
We suppose that the nodes of a multiway tree contain single characters. In the depth-first order sequence of its nodes, a special character ^ has been inserted whenever, during the tree traversal, the move is a backtrack to the previous level.

By this rule, the tree in the figure is represented as:
afg^^c^bd^e^^^
Define the syntax of the string and write a convenience initializer to construct an MTree from a string.
Example:
MTree(string: "afg^^c^bd^e^^^")
Result:
MTree("a", List(MTree("f", List(MTree("g"))), MTree("c"), MTree("b", List(MTree("d"), MTree("e")))))
Implementation:
extension MTree {
convenience init(string: String) {
...
}
}
Now, implement the CustomStringConvertible protocol on MTree.
Example:
MTree("a", List(MTree("f", List(MTree("g"))), MTree("c"), MTree("b", List(MTree("d"), MTree("e"))))).description
Result:
"afg^^c^bd^e^^^"
Implementation:
extension MTree: CustomStringConvertible {
var description: String {
...
}
}
P71 (*) Determine the internal path length of a tree.
We define the internal path length of a multiway tree as the total sum of the path lengths from the root to all nodes of the tree. By this definition, the tree in the figure of problem P70 has an internal path length of 9. Write a computed variable internalPathLength to return that sum.
Example:
MTree(string: "afg^^c^bd^e^^^").internalPathLength
Result:
9
Implementation:
extension MTree {
var internalPathLength: Int {
...
}
}
P72 (*) Construct the post-order sequence of the tree nodes.
Write a method postOrder() which constructs the post-order sequence of the nodes of a multiway tree. The result should be a List.
Example:
MTree(string: "afg^^c^bd^e^^^").postOrder()
Result:
List("g", "f", "c", "d", "e", "b", "a")
Implementation:
extension MTree {
func postOrder() -> List<T> {
...
}
}
P73 (**) Lisp-like tree representation.
There is a particular notation for multiway trees in Lisp. Lisp is a prominent functional programming language. In Lisp almost everything is a list. Our example tree would be represented in Lisp as:
(a (f g) c (b d e))
The following pictures give some more examples:
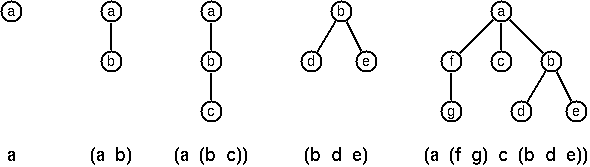
Note that in the “lispy” notation, a node with successors (children) in the tree is always the first element in a list, followed by its children. The “lispy” representation of a multiway tree is a sequence of atoms and parentheses ‘(‘ and ‘)’, with the atoms separated by spaces. We can represent this syntax as a String. Write a method lispyString() which constructs a “lispy string” from an MTree.
Example:
MTree("a", List(MTree("b", List(MTree("c"))))).lispyString()
Result:
"(a (b c))"
Implementation:
extension MTree {
func lispyString() -> String {
...
}
}
As a second, even more interesting, exercise try to write another convenience initializer that takes a “lispy” string and turns it into a multiway tree.
Example:
MTree(lispyString: "(a (b c))")
Result:
MTree("a", List(MTree("b", List(MTree("c")))))
Implementation:
extension MTree {
convenience init(lispyString: String) {
...
}
}
[Note: Much of this problem is taken from the wording of the same problem in the Prolog set. This is certainly one way of looking at Lisp notation, but it’s not how the language actually represents that syntax internally.]
Section 6: Graphs
A graph is defined as a set of nodes and a set of edges, where each edge is a pair of nodes.
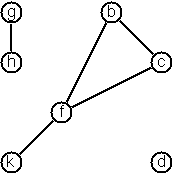
We will define our generic graph as follows:
class Graph<T, U> {
var direction: GraphDirection {
return .Indirected
}
var nodes: List<T>?
var edges: List<(T, T, U)>?
}
class Digraph<T, U> : Graph<T, U> {
override var direction: GraphDirection { return .Directed }
}
enum GraphDirection {
case Indirected
case Directed
}
There are a few ways to create a graph from primitives. The graph-term form lists the nodes and edges separately:
Graph<String, Int>(
nodes: List("b", "c", "d", "f", "g", "h", "k"),
edges: List(("b", "c"), ("b", "f"), ("c", "f"), ("f", "k"), ("g", "h"))
)
The adjacency-list form associates each node with its adjacent nodes. In an undirected graph, care must be taken to ensure that all links are symmetric—if b is adjacent to c, c must also be adjacent to b.
Graph<String, Int>(adjacentList: List(
("b", List("c", "f")),
("c", List("b", "f")),
("d", nil),
("f", List("b", "c", "k")),
("g", List("h")),
("h", List("g")),
("k", List("f"))
))
The representations we introduced so far are bound to our implementation and therefore well suited for automated processing, but their syntax is not very user-friendly. Typing the terms by hand is cumbersome and error-prone.
We can define a more compact and “human-friendly” notation as follows: A graph is represented by a string of terms of the type X or Y-Z separated by commas. The standalone terms stand for isolated nodes, the Y-Z terms describe edges. If an X appears as an endpoint of an edge, it is automatically defined as a node. Our example could be written as:
[b-c, f-c, g-h, d, f-b, k-f, h-g]
We call this the human-friendly form. As the example shows, the list does not have to be sorted and may even contain the same edge multiple times. Notice the isolated node d.
Directed Graphs
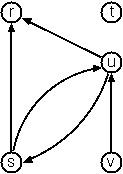
When the edges of a graph are directed, we call them arcs. These are represented by ordered pairs. Such a graph is called directed graph. To represent a directed graph, the forms discussed above are slightly modified. The example graph above is represented as follows.
Graph-term form:
Digraph<String, Int>(
nodes: List("r", "s", "t", "u", "v"),
edges: List(("s", "r"), ("s", "u"), ("u", "r"), ("u", "s"), ("v", "u"))
)
Adjacency-list form:
Digraph<String, Int>(adjacentList: List(
("r", nil),
("s", List("r", "u")),
("t", nil),
("u", List("r", "s")),
("v", List("u"))
))
Human-friendly form:
[s>r, t, u>r, s>u, u>s, v>u]
Labeled Graphs
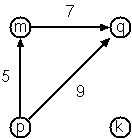
Finally, graphs and digraphs may have additional information attached to nodes and edges (arcs). For the nodes, this is no problem, as we can put any type into them. On the other hand, for edges we have to extend our notation. Graphs with additional information attached to edges are called labeled graphs.
In our Graph class definition above, we store edges as a list of tuples where each tuple contains two nodes of type T and a label of type U, so we can handle both non-labeled and labeled graphs (for non-labeled graphs you can set a default value of zero, for example).
var edges: List<(T, T, U)>?
Graph-term form:
Digraph(
nodes: List("k", "m", "p", "q"),
labeledEdges: List(("m", "q", 7), ("p", "m", 5), ("p", "q", 9))
)
Note that Swift can infer the types of both nodes and edges in this case, as long as there is at least one edge.
Adjacency-list form:
Digraph(adjacentLabeledList: List(
("k", nil),
("m", List(("q", 7))),
("p", List(("m", 5), ("q", 9))),
("q", nil)
))
Note that Swift can infer the types of both nodes and edges in this case, as long as there is at least one edge.
Human-friendly form:
[p>q/9, m>q/7, k, p>m/5]
The notation for labeled graphs can also be used for so-called multi-graphs, where more than one edge (or arc) is allowed between two given nodes.
P80 (***) Conversions.
Write methods to generate the graph-term and adjacency-list forms from both Graph and Digraph. Implement CustomStringConvertible to output the human-friendly form. Then, write convenience initializers to create graphs from human-friendly form strings.
Hint: You might need separate functions for labeled and unlabeled graphs.
Example #1:
Graph(string: "[b-c, f-c, g-h, d, f-b, k-f, h-g]").toTermForm()
Result:
(
List("d", "k", "h", "c", "f", "g", "b"),
List(("h", "g"), ("k", "f"), ("f", "b"), ("g", "h"), ("f", "c"), ("b", "c"))
)
Implementation:
extension Graph {
convenience init(string: String) {
...
}
func toTermForm() -> (List<T>, List<(T, T)>?) {
...
}
}
Example #2:
Digraph(labeledString: "[p>q/9, m>q/7, k, p>m/5]").toAdjacentFormLabeled()
Result:
List(
("m", List(("q", 7))),
("p", List(("m", 5), ("q", 9))),
("k", nil),
("q", nil)
)
Implementation:
extension Digraph {
convenience init(labeledString: String) {
...
}
func toAdjacentFormLabeled() -> List<(T, List<(T, U)>?)> {
...
}
}
P81 (**) Path from one node to another one.
Write a method named findPaths() to find acyclic paths from one node to another in a graph. The method should return all paths.
Example #1:
Digraph(labeledString: "[p>q/9, m>q/7, k, p>m/5]").findPathsFrom("p", to: "q")
Result:
List(List("p", "q"), List("p", "m", "q"))
Example #2:
Digraph(labeledString: "[p>q/9, m>q/7, k, p>m/5]").findPathsFrom("p", to: "k")
Result:
nil
Implementation:
extension Digraph {
func findPathsFrom(from: T, to: T) -> List<List<T>>? {
...
}
}
Implement for both Graph and Digraph.
P82 (*) Cycle from a given node.
Write a method named findCyclesFrom() to find closed paths (cycles) starting at a given node in a graph. The method should return all cycles.
Example:
Graph(string: "[b-c, f-c, g-h, d, f-b, k-f, h-g]").findCyclesFrom("f")
Result:
List(List("f", "c", "b", "f"), List("f", "b", "c", "f"))
Implementation:
extension Graph {
func findCyclesFrom(from: T) -> List<List<T>>? {
...
}
}
Implement for both Graph and Digraph.
P83 (**) Construct all spanning trees.
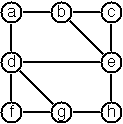
Write a method spanningTrees() to construct all spanning trees of a given graph. The method should return a linked list of sub-graphs for each spanning tree.
With this method, find out how many spanning trees there are for the graph depicted above. When you have a correct solution for the spanningTrees method, use it to define two other useful methods: isTree() and isConnected(). Both are five-minute tasks!
The graph above can be constructed as:
Graph(
nodes: List("a", "b", "c", "d", "e", "f", "g", "h"),
edges: List(("a", "b"), ("a", "d"), ("b", "c"), ("b", "e"),
("c", "e"), ("d", "e"), ("d", "f"), ("d", "g"),
("e", "h"), ("f", "g"), ("g", "h"))
)
Example:
Graph(string: "[a-b, b-c, a-c]").spanningTrees()
Result:
List(
Graph(adjacentList: List(("a", List("b")), ("b", List("c")))),
Graph(adjacentList: List(("a", List("c")), ("b", List("c")))),
Graph(adjacentList: List(("a", List("b")), ("a", List("c"))))
)
Implementation:
extension Graph {
func spanningTrees() -> List<Graph<T, U>>? {
...
}
}
Implement for both Graph and Digraph.
P84 (**) Construct the minimal spanning tree.
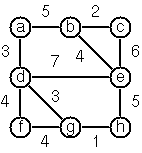
Write a method minimalSpanningTree() to construct the minimal spanning tree of a given labeled graph.
Hint: Use Prim’s Algorithm. A small modification of the solution of P83 does the trick.
The graph above can be constructed as:
Graph(
nodes: List("a", "b", "c", "d", "e", "f", "g", "h"),
labeledEdges: List(("a", "b", 5), ("a", "d", 3), ("b", "c", 2),
("b", "e", 4), ("c", "e", 6), ("d", "e", 7),
("d", "f", 4), ("d", "g", 3), ("e", "h", 5),
("f", "g", 4), ("g", "h", 1))
)
Example:
Graph(labeledString: "[a-b/1, b-c/2, a-c/3]").minimalSpanningTree()
Result:
Graph(adjacentList: List(
("a", List(("b", 1))),
("b", List(("c", 2)))
))
Implementation:
extension Graph {
func minimalSpanningTree() -> Graph<T, U>? {
...
}
}
Implement for both Graph and Digraph.
P85 (**) Graph isomorphism.
Two graphs G1(N1, E1) and G2(N2, E2) are isomorphic if there is a bijection f: N1 ↦ N2 such that for any nodes X, Y of N1, X and Y are adjacent if and only if f(X) and f(Y) are adjacent.
Write a method that determines whether two graphs are isomorphic.
Example:
Graph(string: "[a-b]").isIsomorphicTo(Graph(string: "[5-7]"))
Result:
true
Implementation:
extension Graph {
func isIsomorphicTo<V, W>(graph: Graph<V, W>) -> Bool {
...
}
}
P86 (**) Node degree and graph coloration.
a) Write a method nodeDegrees() that determines the degree of a given node.
Example:
Graph(string: "[a-b, b-c, a-c, a-d]").nodeDegrees("a")
Result:
3
Implementation:
extension Graph {
func nodeDegrees(node: T) -> Int {
...
}
}
b) Write a method that lists all nodes of a graph sorted according to decreasing degree.
Example:
Graph(string: "[a-b, b-c, a-c, a-d]").nodesByDegree()
Result:
List("a", "c", "b", "d")
Implementation:
extension Graph {
func nodesByDegree() -> List<T> {
...
}
}
c) Use Welsh-Powell algorithm to paint the nodes of a graph in such a way that adjacent nodes have different colors. Make a method coloredNodes() that returns a linked list of tuples, each of which contains a node and an integer representing its color.
Example:
Graph(string: "[a-b, b-c, a-c, a-d]").coloredNodes()
Result:
List(("a", 1), ("b", 2), ("c", 3), ("d", 2))
Implementation:
extension Graph {
func coloredNodes() -> List<(T, Int)> {
...
}
}
P87 (**) Depth-first order graph traversal.
Write a method that generates a depth-first order graph traversal sequence. The starting point should be specified, and the output should be a list of nodes that are reachable from this starting point (in depth-first order).
Example:
Graph(string: "[a-b, b-c, e, a-c, a-d]").depthFirstTraversalFrom("d")
Result:
List("c", "b", "a", "d")
Implementation:
extension Graph {
func depthFirstTraversalFrom(node: T) -> List<T> {
...
}
}
P88 (**) Connected components.
Write a function that splits a graph into its connected components.
Example:
Graph(string: "[a-b, c]").splitGraph()
Result:
List(
Graph(nodes: List("a", "b"), edges: List(("a", "b"))),
Graph(nodes: List("c"), edges: nil)
)
Implementation:
extension Graph {
func splitGraph() -> List<Graph<T, U>> {
...
}
}
P89 (**) Bipartite graphs.
Write a function that determines whether a given graph is bipartite.
Example #1:
Digraph(string: "[a>b, c>a, d>b]").isBipartite()
Result:
true
Example #2:
Graph(string: "[a-b, b-c, c-a]").isBipartite()
Result:
false
Example #3:
Graph(string: "[a-b, b-c, d]").isBipartite()
Result:
true
Example #4:
Graph(string: "[a-b, b-c, d, e-f, f-g, g-e, h]").isBipartite()
Result:
false
Implementation:
extension Graph {
func isBipartite() -> Bool {
...
}
}
Apendix 6A (**) DOT.
Implement a toDOT method on both Graph and Digraph that returns a string containing the graph representation in DOT format.
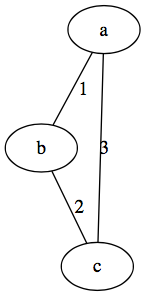
Example #1:
Graph(labeledString: "[a-b/1, b-c/2, a-c/3]").toDOT()
Result:
graph G {
a -- b [label=1]
b -- c [label=2]
a -- c [label=3]
}
Example #2:
Digraph(labeledString: "[p>q/9, m>q/7, k, p>m/5]").toDOT()
Result:
digraph G {
p -> q [label=9]
m -> q [label=7]
p -> m [label=5]
}
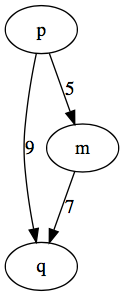
Implementation:
extension Graph {
func toDOT() -> String {
...
}
}
Check if your graph DOT output is correct here: Viz.js DOT
Section 7: Miscellaneous Problems
For the sake of organization, we will create a stub structure to hold our miscellaneous mehtods from this section.
struct MiscellaneousProblems { }
Solutions will be added as static methods.
P90 (**) Eight queens problem
This is a classical problem in computer science. The objective is to place eight queens on a chessboard so that no two queens are attacking each other; i.e., no two queens are in the same row, the same column, or on the same diagonal.
Hint: Represent the positions of the queens as a list of numbers 1..n. Example: List(4, 2, 7, 3, 6, 8, 5, 1) means that the queen in the first column is in row 4, the queen in the second column is in row 2, etc. Use the generate-and-test paradigm.
Implementation:
extension MiscellaneousProblems {
static func eightQueens() -> List<Int> {
...
}
}
P91 (**) Knight’s tour.
Another famous problem is this one: How can a knight jump on an NxN chessboard in such a way that it visits every square exactly once?
Hints: Represent the squares by pairs of their coordinates of the form (X, Y), where both X and Y are integers between 1 and N. Write a function jumps(N, (X, Y)) to list the squares that a knight can jump to from (X, Y) on a NxN chessboard. And finally, represent the solution of our problem as a list of (X, Y) knight positions (the knight’s tour).
Implementation:
extension MiscellaneousProblems {
static func knightsTour(n: Int) -> List<(Int, Int)> {
...
}
}
Can you find only “closed tours”, where the knight can jump from its final position back to its starting position?
Implementation:
extension MiscellaneousProblems {
static func closedKnightsTour(n: Int) -> List<(Int, Int)> {
...
}
}
P92 (***) Von Koch’s conjecture.
Several years ago I met a mathematician who was intrigued by a problem for which he didn’t know a solution. His name was Von Koch, and I don’t know whether the problem has been solved since. [The “I” here refers to the author of the original Prolog problems.]
Anyway the puzzle goes like this:
Given a tree with N nodes (and hence N-1 edges), find a way to enumerate the nodes from 1 to N and, accordingly, the edges from 1 to N-1 in such a way, that for each edge K the difference of its node numbers is equal to K. The conjecture is that this is always possible.
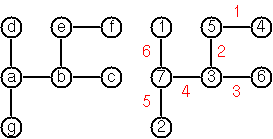
For small trees the problem is easy to solve by hand. However, for larger trees, and 14 is already very large, it is extremely difficult to find a solution. And remember, we don’t know for sure whether there is always a solution!
Write a method for our Tree class that calculates a numbering scheme for the tree and returns a labeled graph. What is the solution for the larger tree pictured below?
Implementation:
extension Tree {
func vonKochsConjecture() -> Graph<Int, Int> {
...
}
}
P93 (***) An arithmetic puzzle.
Given a list of integer numbers, find a correct way of inserting arithmetic signs (operators) such that the result is a correct equation. Example: With the list of numbers List(2,3,5,7,11) we can form the equations 2-3+5+7 = 11 or 2 = (3*5+7)/11 (and ten others!).
Implementation:
extension MiscellaneousProblems {
static func equation(list: List<Int>) -> String {
...
}
}
P94 (***) Generate K-regular simple graphs with N nodes.
In a K-regular graph all nodes have a degree of K; i.e. the number of edges incident in each node is K. How many (non-isomorphic!) 3-regular graphs with 6 nodes are there? Use the Viz.js tool to validate your graphs.
Implementation:
extension Graph {
class func makeRegularGraphs(k: Int, value: T) -> List<Graph<T, U>> {
...
}
}
P95 (**) English number words.
On financial documents, like checks, numbers must sometimes be written in full words. Example: 175 must be written as one-seven-five. Write a function to convert (non-negative) integer numbers to full words.
Implementation:
extension Miscellaneous {
static func fullWords(number: Int) -> String {
...
}
}
P96 (**) Syntax checker.
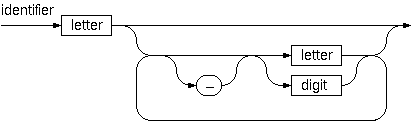
In a certain programming language (Ada) identifiers are defined by the syntax diagram (railroad chart) above. Transform the syntax diagram into a system of syntax diagrams which do not contain loops; i.e. which are purely recursive. Using these modified diagrams, write a function isIdentifier() that can check whether or not a given string is a legal identifier.
Implementation:
extension Miscellaneous {
static func isIdentifier(string: String) -> Bool {
...
}
}
P97 (**) Sudoku.
Sudoku puzzles go like this:
Problem statement: Solution:
. . 4 | 8 . . | . 1 7 9 3 4 | 8 2 5 | 6 1 7
| | | |
6 7 . | 9 . . | . . . 6 7 2 | 9 1 4 | 8 5 3
| | | |
5 . 8 | . 3 . | . . 4 5 1 8 | 6 3 7 | 9 2 4
--------+---------+-------- --------+---------+--------
3 . . | 7 4 . | 1 . . 3 2 5 | 7 4 8 | 1 6 9
| | | |
. 6 9 | . . . | 7 8 . 4 6 9 | 1 5 3 | 7 8 2
| | | |
. . 1 | . 6 9 | . . 5 7 8 1 | 2 6 9 | 4 3 5
--------+---------+-------- --------+---------+--------
1 . . | . 8 . | 3 . 6 1 9 7 | 5 8 2 | 3 4 6
| | | |
. . . | . . 6 | . 9 1 8 5 3 | 4 7 6 | 2 9 1
| | | |
2 4 . | . . 1 | 5 . . 2 4 6 | 3 9 1 | 5 7 8
Every spot in the puzzle belongs to a (horizontal) row and a (vertical) column, as well as to one single 3x3 square (which we call “square” for short). At the beginning, some of the spots carry a single-digit number between 1 and 9. The problem is to fill the missing spots with digits in such a way that every number between 1 and 9 appears exactly once in each row, in each column, and in each square.
a) Write a method that, given a list of 81 integers (we will use 0 to indicate a blank position), returns a list of 81 integers with the puzzle solution.
Example:
Miscellaneous.sudoku(List(0, 0, 4, 8, 0, 0, 0, 1, 7, 6, 7, 0, ...))
Result:
List(9, 3, 4, 8, 2, 5, 6, 1, 7, 6, 7, ...)
Implementation:
extension Miscellaneous {
static func sudoku(list: List<Int>) -> List<Int>? {
...
}
}
b) Write a method to validate a sudoku solution.
Implementation:
extension Miscellaneous {
static func isValidSudokuSolution(list: List<Int>) -> Bool {
...
}
}
P98 (***) Nonograms.
Around 1994, a certain kind of puzzles was very popular in England. The “Sunday Telegraph” newspaper wrote:
Nonograms are puzzles from Japan and are currently published each week only in The Sunday Telegraph. Simply use your logic and skill to complete the grid and reveal a picture or diagram.
As a programmer, you are in a better situation: you can have your computer do the work! Just write a little program ;-).
The puzzle goes like this: Essentially, each row and column of a rectangular bitmap is annotated with the respective lengths of its distinct strings of occupied cells. The person who solves the puzzle must complete the bitmap given only these lengths.
Problem statement: Solution:
|_|_|_|_|_|_|_|_| 3 |_|X|X|X|_|_|_|_| 3
|_|_|_|_|_|_|_|_| 2 1 |X|X|_|X|_|_|_|_| 2 1
|_|_|_|_|_|_|_|_| 3 2 |_|X|X|X|_|_|X|X| 3 2
|_|_|_|_|_|_|_|_| 2 2 |_|_|X|X|_|_|X|X| 2 2
|_|_|_|_|_|_|_|_| 6 |_|_|X|X|X|X|X|X| 6
|_|_|_|_|_|_|_|_| 1 5 |X|_|X|X|X|X|X|_| 1 5
|_|_|_|_|_|_|_|_| 6 |X|X|X|X|X|X|_|_| 6
|_|_|_|_|_|_|_|_| 1 |_|_|_|_|X|_|_|_| 1
|_|_|_|_|_|_|_|_| 2 |_|_|_|X|X|_|_|_| 2
1 3 1 7 5 3 4 3 1 3 1 7 5 3 4 3
2 1 5 1 2 1 5 1
For the example above, the problem can be stated as:
let rows = List(List(3), List(2, 1), List(3, 2), List(2, 2), List(6), List(1, 5), List(6), List(1), List(2))
let columns = List(List(1, 2), List(3, 1), List(1, 5), List(7, 1), List(5), List(3), List(4), List(3))
These two lists give the “solid” lengths of the rows and columns, top-to-bottom and left-to-right, respectively.
Published puzzles are larger than this example, e.g. 25x20, and apparently always have unique solutions.
Write a method that given a pair of lists of row lengths and column lengths solves the problem and returns the solutions as a list of tuples (X, Y) indicating the coordinates of each checked square (zero-based starting from the top-left corner).
Implementation:
extension Miscellaneous {
static func nonogram(rows: List<List<Int>>, columns: List<List<Int>>) -> List<(Int, Int)> {
...
}
}
P99 (***) Crossword puzzle.
Given an empty (or almost empty) framework of a crossword puzzle and a set of words. The problem is to place the words into the framework.
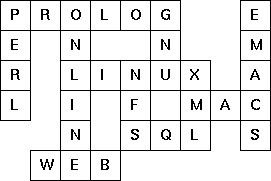
The particular crossword puzzle is specified in a text file which first lists the words (one word per line) in an arbitrary order. Then, after an empty line, the crossword framework is defined. In this framework specification, an empty character location is represented by a dot .. In order to make the solution easier, character locations can also contain predefined character values.
The puzzle above is defined in the file p99a.txt (shown below). Other examples are p99b.txt and p99d.txt. There is also an example of a puzzle (p99c.txt) which does not have a solution.
Example P99A:
LINUX
PROLOG
PERL
ONLINE
GNU
XML
NFS
SQL
EMACS
WEB
MAC
...... .
. . . .
. ..... .
. . . ...
. ... .
...
Words are strings of at least two characters. A horizontal or vertical sequence of character places in the crossword puzzle framework is called a site. Our problem is to find a compatible way of placing words onto sites.
Hints:
(1) The problem is not easy. You will need some time to thoroughly understand it. So, don’t give up too early! And remember that the objective is a clean solution, not just a quick-and-dirty hack!
(2) For efficiency reasons it is important, at least for larger puzzles, to sort the words and the sites in a particular order. For this part of the problem, the solution of P28 may be very helpful.
Ninety-Nine Swift Solutions
If you are interested in sharing your solutions online and/or would like to review somebody else’s solutions, please go to the Ninety-Nine Swift Solutions repository on GitHub and submit a pull request!
Please use the format pXX_username.swift to name your solutions, where XX is the problem number and username is your GitHub username in lower-case.